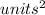Answer:
A = 53.34
Explanation:
To find the length of the rectangle we solve the PLA triangle
Using the Pythagorean theorem we find the PL side.
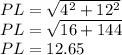
Then the length of the rectangle is 12.65
Now we solve the MALU triangle. Where MU = PL
We use the Pythagorean theorem:

Where LU and MA are unknown.
Finally we solve the triangle MPA
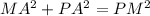
Where PM = LU
So:

Now we have two equations and two unknowns. So we solve the system.
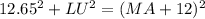 (i)
(i)
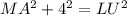 (ii)
(ii)
We introduce (ii) in (i)
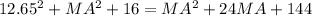
Now we clear MA
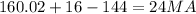

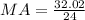
MA = 1.3342 (iii)
Now we introduce (iii) in (ii)
1.3342^2 + 4^2 = LU^2
LU = 4.2166
Now we have the length of the rectangle and also its width.
The area A of a rectangle is:
A = l*w
Where
l = length
w = width
A = 4.2166*12.65
A = 53.34