Question

Consider this equation and the steps taken to solve it.  –9(a – 5) = –18  (distribute)  –9a + 45 = –18  (subtract 45)     –9a = –63  (divide by –9)     a = 7 What steps might you take to verify the solution? Check all that apply. Substitute 7 for a. Pick any value for a and substitute. Simplify the equation after substituting the value for a. Verify that a = 7 is correct when the result is a true statement. Verify that a = 7 is correct when the result is a false statement.

Answer 1

Substitute 7 for a.

Simplify the equation after substituting the value for a.

Verify that a = 7 is correct when the result is a true statement.

Explanation:

Here, the given equation is,,

`-9(a-5)=-18`

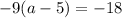
And, after solving it the result is,

a = 7

We can check whether a result is the solution of an equation by substituting the result in the given equation.

If we get a true statement, then the result is the solution of the equation.

Thus, for verifying the solution, steps are as follow,

Step 1 : Substitute 7 ,

-9(7-5) = -18

Step 2 : Simplify the equation after substituting the value of a

-9(2) = -18

Step 3 : Verify that a = 7 is correct when the result is a true statement.

-18 = -18

Answer 2

Substitute 7 for a.

Simplify the equation after substituting the value for a.

Verify that a = 7 is correct when the result is a true statement.

Explanation:

 –9(a – 5) = –18

Distribute

-9a +45 = -18

Subtract 45 from each side

-9a +45-45 = -18-45

-9a = -63

Divide each side by -9

-9a/-9 = -63/-9

a = 7

To check the solution put a =7 back into the original equation

 –9(a – 5) = –18

-9(7-5) = -18

Simplify

-9(2) = -18

-18 = 18

This is true so 7 is the solution