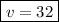Every two triangles are similar. Therefore the sides of triangles are in proportion.
We have the equations:
1.
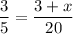 cross multiply
cross multiply
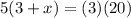 divide both sides by 5
divide both sides by 5
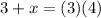
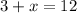 subtract 3 from both sides
subtract 3 from both sides
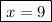
--------------------------------------
2.
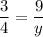 cross multiply
cross multiply
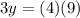
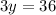 divide both sides by 3
divide both sides by 3
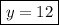
------------------------------------------
3.
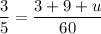
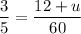 cross multiply
cross multiply
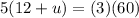 divide both sides by 5
divide both sides by 5
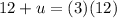
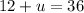 subtract 12 from both sides
subtract 12 from both sides
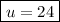
----------------------------------------------
4.
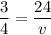 cross multiply
cross multiply
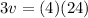
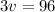 divide both sides by 3
divide both sides by 3