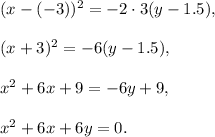Answer:
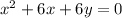
Explanation:
The distance between the parabola focus and the directrix is 3, then
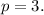
Parabola vertex is placed on the perpendicular line to the directrix and this perpendicular line passes trough the focus. Its equation is x=-3 and parabola vertex coordinates are (-3,1.5).
Branches of the parabola go in negative y-direction, then the equation of the parabola is