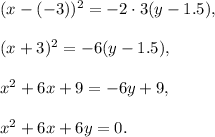Question

The parabola has a focus at (−3, 0) and directrix y = 3. What is the correct equation for the parabola? x2 = −12y x2 = 3y y2 = 3x y2 = −12x

Answer 1

y2=-12x

Explanation:

Answer 2

`x^2+6x+6y=0`

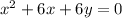
Explanation:

The distance between the parabola focus and the directrix is 3, then

`p=3.`

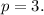
Parabola vertex is placed on the perpendicular line to the directrix and this perpendicular line passes trough the focus. Its equation is x=-3 and parabola vertex coordinates are (-3,1.5).

Branches of the parabola go in negative y-direction, then the equation of the parabola is

`(x-(-3))^2=-2\cdot 3(y-1.5),\\ \\(x+3)^2=-6(y-1.5),\\ \\x^2+6x+9=-6y+9,\\ \\x^2+6x+6y=0.`