Answer:
The slopes for each of the four line segments are
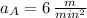 ,
,
 ,
,
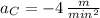 and
and
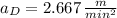 , respectively.
, respectively.
Step-by-step explanation:
There are four line segments:
(i) Line A:
 ,
,
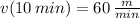
(ii) Line B:
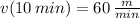 ,
,
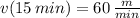
(iii) Line C:
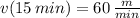 ,
,

(iv) Line D:
 ,
,
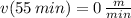
The slope of each line segment represents the acceleration of the particle, which can calculated by the geometrical concept of secant line. Hence, we proceed to determine the acceleration associated with each line segment:
Line A
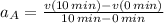

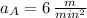
Line B
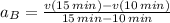


Line C
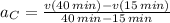
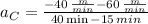
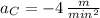
Line D
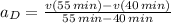
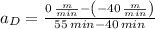
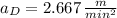
The slopes for each of the four line segments are
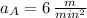 ,
,
 ,
,
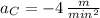 and
and
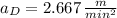 , respectively.
, respectively.