To prove a rhombus you need to show that the sides are congruent and the diagonals are perpendicular.
Sides:
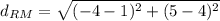
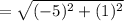
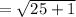
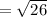
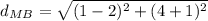
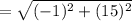
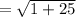
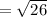
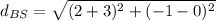

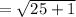
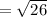
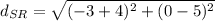
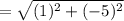
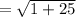
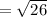
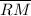 ≅
≅
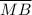 ≅
≅
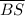 ≅
≅
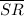
Diagonals:
Use the slope formula:
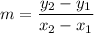
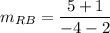
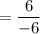
= -1
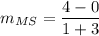
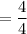
= 1
Slopes are opposite reciprocals so they are perpendicular.
***************************************************************************
All of the sides are congruent and the diagonals are perpendicular so RMBS is a rhombus.