The function f(x)=5^(x-1) is shown on the coordinate plane. Select from the drop down menus to correctly describe the end behavior of f(x)

Question

asked Mar 20, 2019 13.3k views

1 Answer

Nakamura · Answer 1 · 2019-03-25T16:46:39+0000

Answer: The end behavior of the given function is,

$f(x)\rightarrow 0$ as
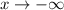
$x\rightarrow -\infty$

And,
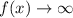$f(x)\rightarrow \infty$ as
$x\rightarrow \infty$

Explanation:

Since, by the property of the graph of the exponential function,

If an exponential function is,
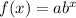
f(x) = ab^x

If b >1 ( increasing function ) then its end behavior is,

$f(x)\rightarrow 0$ as
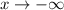
$x\rightarrow -\infty$

And,
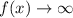$f(x)\rightarrow \infty$ as
$x\rightarrow \infty$

While b < 1 ( decreasing function, then its end behavior is,

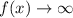$f(x)\rightarrow \infty$ as
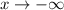
$x\rightarrow -\infty$

And,
$f(x)\rightarrow 0$ as
$x\rightarrow \infty$

Here, given function is,
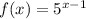
f(x)=5^(x-1)

Since 5 > 1

Therefore, the end behavior of the given function is,

$f(x)\rightarrow 0$ as
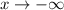
$x\rightarrow -\infty$

And,
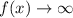$f(x)\rightarrow \infty$ as
$x\rightarrow \infty$