Question

The sides of a triangular field are in the ratio of 5:6: 7. If its perimeter is 3600 m. find the area of that land

Answer 1

Area = 587877.54
`m^(2)`

Explanation:

Let the length of sides of the triangle be represented by a, b and c respectively.

a =
`(5)/(18)` x 3600

= 1000

b =
`(6)/(18)` x 3600

= 1200

c =
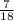`(7)/(18)` x 3600

= 1400

The length of the sides of the triangle are: 1000 m , 1200 m, 1400 m.

Perimeter = a + b + c

= 1000 + 1200 + 1400

= 3600

The area of the land can be determined by;

Area of a triangle =
`√((s*(s-a)* (s-b)* (s-c)))`

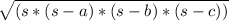
where: s is the semi-perimeter of the triangle and a, b and c are the length of sides respectively.

s =
`(perimeter)/(2)`

=
`(3600)/(2)`

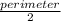
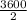
s = 1800

Area =
`√((1800(1800 - 1000)*(1800 - 1200)*(1800 - 1400)))`

=
`√((1800*800*600*400))`

=
`√(345600000000)`

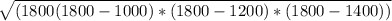
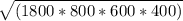
= 587877.54

Area = 587877.54
`m^(2)`

The area of the triangle is 587877.54
`m^(2)`.