ANSWER
The vertex form is
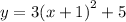
Step-by-step explanation
We want to write
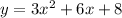
in the vertex form which of the form
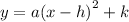
We achieve this BG completing the square.
We proceed as follows,
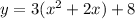
We add and subtract half the coefficient of x multiplied by a factor of 3 which is
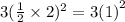
This gives us,
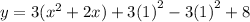
We still factor 3 out of the first two terms to get,
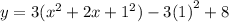
We now got a perfect square, which factors to,
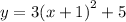
The equation is now in the vertex form.