Question

-. A 2kg cart moving to the right at 5m/s collides with an 8kg cart at rest. As a

result of the collision, the cart locks together. What is the velocity of the carts
after the event?

Answer 1

The velocity of the carts after the event is 1 m/s

Step-by-step explanation:

Law Of Conservation Of Linear Momentum

The total momentum of a system of bodies is conserved unless an external force is applied to it. The formula for the momentum of a body with mass m and speed v is

P=mv.

If we have a system of bodies, then the total momentum is the sum of the individual momentums:

`P=m_1v_1+m_2v_2+...+m_nv_n`

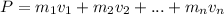
If a collision occurs and the velocities change to v', the final momentum is:

`P'=m_1v'_1+m_2v'_2+...+m_nv'_n`

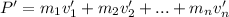
Since the total momentum is conserved, then:

P = P'

In a system of two masses, the equation simplifies to:

`m_1v_1+m_2v_2=m_1v'_1+m_2v'_2`

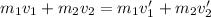
If both masses stick together after the collision at a common speed v', then:

`m_1v_1+m_2v_2=(m_1+m_2)v'`

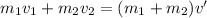
The common velocity after this situation is:

`\displaystyle v'=(m_1v_1+m_2v_2)/(m_1+m_2)`

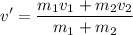
The m1=2 kg cart is moving to the right at v1=5 m/s. It collides with an m2= 8 kg cart at rest (v2=0). Knowing they stick together after the collision, the common speed is:

`\displaystyle v'=(2*5+8*0)/(2+8)=(10)/(10)=1`

The velocity of the carts after the event is 1 m/s