Answer:
4). m∠DAE = 23°
5). m(∠BAE) = 29.5°
Explanation:
4). "Angle formed by the intersection of two tangents and secants outside the circle is half of the difference of intercepted arcs"
m∠DAE =
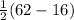
=
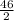
= 23°
5). Following the same rule as in question 4,
m(∠BAE) =
![(1)/(2) [m(\text{arc BE})-m(\text{arc CD})]](https://img.qammunity.org/2022/formulas/mathematics/college/yirfejthmi8belwvj2q1qdpuruc1pgvk1b.png)
=
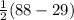
=
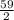
= 29.5°