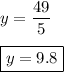Question

Find the exact value of y

Answer 1

Look at the picture.

Use the Pythagorean theorem to solve h:

`h^2+5^2=7^2`

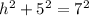
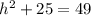`h^2+25=49` subtract 25 from both sides

`h^2=24\to h=√(24)`

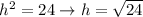
ΔADC and ΔCDB are similar. Therefore the sides are in proportion:

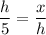`(h)/(5)=(x)/(h)` cross multiply

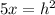`5x=h^2` put the value of h

`5x=(√(24))^2`

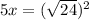
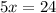`5x=24` divide both sides by 5

`x=4.8`

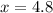
y = 5 + x → y = 5 + 4.8 = 9.8

Answer: y = 9.8

Or other method. ΔADC and ΔACB are similar. Therefore the sides are in proportion:

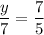`(y)/(7)=(7)/(5)` multiply both sides by 7

`y=(49)/(5)\\\\\boxed{y=9.8}`