Answer:
D
Explanation:
A) True. Alternate interior angles are congruent so

B) True. Considering the sum of these three angles is equal to a straight angle. Since ∠a+∠d supplementary to ∠e
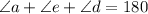
C) True. Since the line segments form a triangle having a (black) line as triangle base.
D) False. ∠b is congruent to its corresponding angle, and ∠e is not its corresponding angle. The corresponding angle of ∠b is the angle vertex opposed to ∠d (not identified).