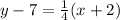Slope-intercept form:
y = mx + b "m" is the slope, "b" is the y-intercept (it's relevant later)
Point-slope form:
y - y₁ = m(x - x₁) "m" is the slope
For lines to be perpendicular, their slopes have to be the opposite/negative reciprocal (flipped sign and number)
For example:
slope is 2
perpendicular line's slope is -1/2
slope is -4/5
perpendicular line's slope is 5/4
Since the given line's slope is -4, the perpendicular line's slope is 1/4.
m = 1/4
(x₁ , y₁) = (-2, 7)
Now plug this into the equation:
y - y₁ = m(x - x₁)
y - 7 = 1/4(x - (-2))