Question

Based on the polynomial reminder theorem, what is the value of the function when x= -5

F (x)= x^4 + 12x^3 + 30x^2 - 12x + 70

Answer 1

`f(-5)=` 5

Explanation:

According to the polynomial remainder theorem, when a polynomial f(x) is divided by a linear polynomial (x - a), the remainder of that division will be equal to f(a).

Therefore, substituting the value of x as -5 in the given function to find its value:

`f(x)` =
`x^4 + 12x^3 + 30x^2 - 12x + 70`

`f(-5)` =
`(-5)^4 + 12(-5)^3 + 30(-5)^2 - 12(-5) + 70`

`f(-5)` =
`625+(-1500)+750-(-60)+70`

`f(-5)` =
`5`

Therefore, the value of the given function when x = -5 is 5.

Answer 2

-15

Explanation:

Given is a polynomial in x

`F (x)= x^4 + 12x^3 + 30x^2 - 12x + 70`

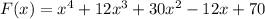
We have to find the remainder when the above polynomial is divided by x+5

Remainder theorem says that f(x) gives remainder R when divided by polynomial x-a means f(a) = R

Applying the above theorem we can say that value of the function when x =-5

= Remainder when f is divided by x+5

= F(-5)

Substitute the value of -5 in place of x

= (-5)^4 + 12(-5)^3 + 30(-5)^2 - 12(-5) + 70

= 625-1500+750+60+70

= 5

Hence answer is 5