Question

Crystal is writing a coordinate proof to show that the diagonals of a parallelogram bisect each other. She starts by assigning coordinates as given. A parallelogram graphed on a coordinate plane. The parallelogram is labeled A B C D. The coordinates of vertex A are 0 comma 0. The coordinates of vertex B a comma 0. The coordinates of vertex C are not labeled. The coordinates of vertex D are b comma c. Diagonals A C and B D intersect at point E whose coordinates are not labeled. Drag and drop the correct answer into each box to complete the proof. The coordinates of point C are (a + b,). The coordinates of the midpoint of diagonal AC¯¯¯¯¯ are ( a+b2 ,). The coordinates of the midpoint of diagonal BD¯¯¯¯¯ are (a+b2, c2) . AC¯¯¯¯¯ and BD¯¯¯¯¯ intersect at point E with coordinates (, c2 ). By the definition of midpoint, ≅CE¯¯¯¯¯ and BE¯¯¯¯¯≅ . Therefore, diagonals AC¯¯¯¯¯ and BD¯¯¯¯¯ bisect each other.

Answer 1

the coordinate point C are (a+b,c)

The coordinates of the midpoint of diagonal AC¯¯¯¯¯ are (a+b/2, c/2)

The coordinates of the midpoint of diagonal BD¯¯¯¯¯ are (a+b/2, c/2)

AC¯¯¯¯¯ and BD¯¯¯¯¯ intersect at point E with coordinates ​(a+b/2, c/2)​

By the definition of midpoint, AE¯¯¯¯¯≅CE¯¯¯¯¯and BE¯¯¯¯¯≅DE¯¯¯¯¯

Explanation:

Answer 2

Answer: The coordinates of the midpoint of diagonal AC are
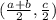`((a+b)/(2) , (c)/(2) )`. The coordinates of the midpoint of diagonal BD are
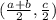`((a+b)/(2) , (c)/(2) )` AC and BD intersect at point E with coordinates
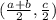`((a+b)/(2) , (c)/(2) )`. By the definition of midpoint, CE ≅ EA and BE ≅ ED Therefore, diagonals AC and BD bisect each other.

Explanation:

Since, here the coordinates of A ≡ (0,0) B ≡ (a, 0) D≡ ( b,c)

And, here ABCD is the parallelogram.

Therefore AB = CD

If y is the y-coordinate of C Then C≡(a+b, y)

⇒
`a^2 + 0 = (a)^2 + (y-c)^2`

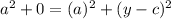
⇒ y =c

Thus, C≡(a+b, c)

The coordinates of the midpoint of diagonal AC are,

`((a+b)/(2) , (c)/(2) )`

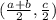
And, The coordinates of the midpoint of diagonal BD are,

`((a+b)/(2) , (c)/(2) )`

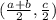
Since, by the below diagram AC and BD are intersecting at point E,

Where the coordinates of E are,

`((a+b)/(2) , (c)/(2) )`

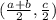
Thus, E is the mid point of Both the segments AC and BD

Because, BE = ED and AE = EC

Therefore, we can say that both AC and BD bisect each other.