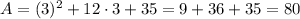1. Area of the original patio: 35 ft^2
The original patio has is a rectangle with length = 7 feet and width = 5 feet. The area of a rectangle is given by the product between length and width:
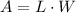
Therefore, since in this case L=7 and W=5, the area of the original patio is
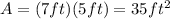
2. Area of section A: 7x ft^2
Section A is also a rectangle, with length = 7 feet and width = x. Therefore, the area of this section is equal to:

3. Area of section B: 5x ft^2
Section B is also a rectangle, with length = x and width = 5 feet. Therefore, the area of this section is equal to:
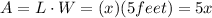
4. Area of section C:
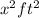
Section C is a square, with side equal to x. The area of a square is equal to the square of the length of the side:

therefore, in this case, since L = x, the area of this section is
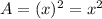
5. Total area of the new patio using addition:
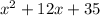 ft^2
ft^2
The total area of the new patio is equal to the sum of the four areas calculated in the previous sections:
 ft^2
ft^2
6. Total area of the new patio using multiplication:
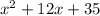
The total area of the new patio is equal to the product between the length (7+x) and the width (5+x):
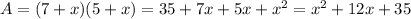 ft^2
ft^2
7. Yes
As we can see by comparing the area calculated in 5. and the area calculated in 6., the two areas are equal.
8. 80 ft^2
We already have the formula for the area of the new patio:
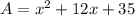
If we substitute x=3, we find the value of the area: