Question

A freight train left Miami and traveled toward the fueling station at an average speed of 60 mph. A passenger train left three hours later and traveled in the same direction but with an average speed of 72 mph. find the number of hours the freight train traveled before the passenger train caught up.

a. 12
b. 15
c. 18
d. 21

Answer 1

sorry im answering late but the answer is C. 18

Step-by-step explanation:

60 x 18 = 1,080

72 started 3 hours later so that means you subtract 3 from 18 which equals 15 and 72 x 15 = 1,080

ur answer is 18

Answer 2

The correct option is b. 15

Step-by-step explanation:

We are given that a freight train travels at an average speed of 60 mph.

Also we are given that the average speed of passenger train is 72 mph.

We are also given that the freight train leaves 3 hours before passenger train. So the number of miles covered by freight train in 3 hours is:

`3 * 60 = 180` miles.

Let X be the number of hours it takes the passenger train to catch up the freight train.

Therefore, we have:

`180 + 60 * X = 72 * X`

`72X-60X = 180`

`12X=180`

`X=(180)/(12)`

`X=15`

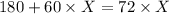
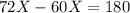
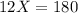
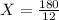
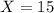
Therefore, the passenger train will take 15 hours to catch up the freight train.