ANSWER
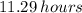
EXPLANATION
The exponential function that models cell duplication in the lab is given as
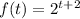
We want to determine the time it will take for the cells to increase to
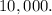
In other words, we want to find the value of
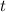
when
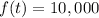
This gives us the equation,
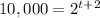
Recall that,
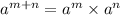
We apply this property to the right hand side to obtain,
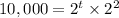
This implies that,
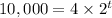
We divide both sides by 4 to get,
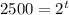
We take the antilogarithm of both sides to base 10 to get,
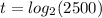
This implies that,
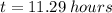
to the nearest hundredth.