Question

1.    An AP has a common difference of 3.  Given that the nth term is 32, and the sum of the first n terms is 185, calculate the value of n.

​

Answer 1

The value of n is 10

Explanation:

The formula of the nth term of the arithmetic progression is a
`_(n)` = a + (n - 1)d

• a is the first term

• d is the common difference between each 2 consecutive terms

• n is the position of the term

The formula of the sum of nth terms is S
`_(n)` =
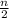`(n)/(2)` [2a + (n - 1)d]

∵ An AP has a common difference of 3

∴ d = 3

∵ The nth term is 32

∴ a
`_(n)` = 32

→ Substitute them in the 1st rule above

∵ 32 = a + (n - 1)3

∴ 32 = a + 3(n) - 3(1)

∴ 32 = a + 3n - 3

→ Add 3 to both sides

∴ 35 = a + 3n

→ Switch the two sides

∴ a + 3n = 35

→ Subtract 3n from both sides

∴ a = 35 - 3n ⇒ (1)

∵ The sum of the first n terms is 185

∴ S
`_(n)` = 185

→ Substitute the value of S
`_(n)` and d in the 2nd rule above

∵ 185 =
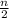`(n)/(2)` [ 2a + (n - 1)3]

∴ 185 =
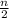`(n)/(2)` [2a + 3(n) - 3(1)]

∴ 185 =
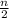`(n)/(2)` [2a + 3n - 3]

→ Multiply both sides by 2

∴ 370 = n(2a + 3n - 3)

∴ 370 = 2an + 3n² - 3n

→ Substitute a by equation (1)

∴ 370 = 2n(35 - 3n) + 3n² - 3n

∴ 370 = 70n - 6n²+ 3n² - 3n

→ Add the like terms in the right side

∵ 370 = -3n² + 67n

→ Add 3n² to both sides

∴ 3n² + 370 = 67n

→ Subtract 67 from both sides

∴ 3n² - 67n + 370 = 0

→ Use your calculator to find n

∴ n = 10 and n = 37/3

∵ n must be a positive integer ⇒ 37/3 neglecting

∴ n = 10

∴ The value of n is 10