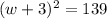Question

Determine the value of c that will result in a perfect square trinomial.
w^2+6w+ c =130+c

Answer 1

The value of c that will result in a perfect square trinomial is (3)^2 or 9

The perfect square trinomial is:
`(w+3)^2=139`

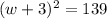
Explanation:

We need to determine the value of c that will result in a perfect square trinomial.

`w^2+6w+ c =130+c`

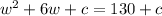
Perfect square trinomial are of form:
`a^2+2ab+b^2=(a+b)^2`

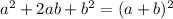
Now, the equation given is:

`w^2+6w+ c =130+c`

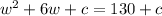
Looking at the term 6w, we can write it as 2(w)(3)

We are given: a = w, 2ab = 2(w)(3) so, b will be: (3)^2

So, we will be adding (3)^2 on both sides

`w^2+6w+ c=130+c\\w^2+2(w)(3)+ (3)^2 =130+(3)^2\\The\:left\:side\:becomes: a^2+2ab+b^2\\We\:can\:write\:it\:as: (a+b)^2\\We\:have\:a=w\: and\: b=3\\(w+3)^2=130+9\\(w+3)^2=139`

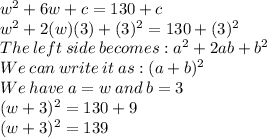
So, The value of c that will result in a perfect square trinomial is (3)^2 or 9

The perfect square trinomial is:
`(w+3)^2=139`