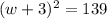Answer:
The value of c that will result in a perfect square trinomial is (3)^2 or 9
The perfect square trinomial is:
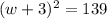
Explanation:
We need to determine the value of c that will result in a perfect square trinomial.
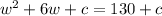
Perfect square trinomial are of form:
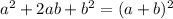
Now, the equation given is:
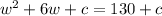
Looking at the term 6w, we can write it as 2(w)(3)
We are given: a = w, 2ab = 2(w)(3) so, b will be: (3)^2
So, we will be adding (3)^2 on both sides
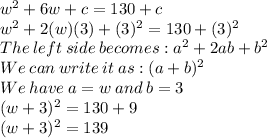
So, The value of c that will result in a perfect square trinomial is (3)^2 or 9
The perfect square trinomial is: