Answer:
Option 4 which is 1,430.
Explanation:
Step 1
In this this step we will break up the terms in the summation symbol using the rules for manipulation summations.
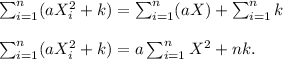
This means that for our case, the sum can be simplified to be,
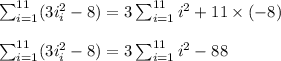
Step 2
In this step we use the formula for the sum of the first n squares to evaluate the first part of the sum in step 2. The formula for the sum of the first n squares is,
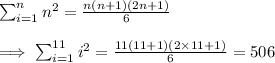
Step 3
In this step we use the result from step 1 to evaluate the sum.

The correct answer is Option 4,which is 1,430.