Question

Evaluate (precalculus)

Answer 1

`\boxed{\boxed{\sum_(i=1)^(11)(3i^2-8)=1430}}`

Explanation:

The given expression is,

`\sum_(i=1)^(11)(3i^2-8)`

`=\sum_(i=1)^(11)(3i^2)-\sum_(i=1)^(11)(8)`

`=3\sum_(i=1)^(11)(i^2)-\sum_(i=1)^(11)(8)`

we know that,

`\sum_(i=1)^(n)i^2=(n(n+1)(2n+1))/(6)` and

`\sum_(i=1)^(n)c=cn,\text{ Where c is a constant}`

Hence,

`3\sum_(i=1)^(11)(i^2)-\sum_(i=1)^(11)(8)=3\left((11(11+1)(2(11)+1))/(6)\right)-8(11)`

`=3\left((11(12)(23))/(6)\right)-8(11)`

`=3\left(506}\right)-8(11)`

`=1518-88`

`=1430`

Answer 2

Option 4 which is 1,430.

Explanation:

Step 1

In this this step we will break up the terms in the summation symbol using the rules for manipulation summations.

`\sum_(i=1)^(n)(aX^2_i+k)=\sum_(i=1)^(n)(aX)+\sum_(i=1)^(n)k\\\\\sum_(i=1)^(n)(aX^2_i+k)=a\sum_(i=1)^(n)X^2+nk.`

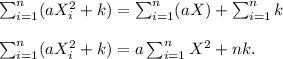
This means that for our case, the sum can be simplified to be,

`\sum_(i=1)^(11)(3i^2_i-8)=3\sum_(i=1)^(11)i^2+11*(-8)\\\\\sum_(i=1)^(11)(3i^2_i-8)=3\sum_(i=1)^(11)i^2-88`

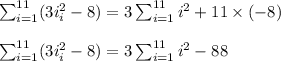
Step 2

In this step we use the formula for the sum of the first n squares to evaluate the first part of the sum in step 2. The formula for the sum of the first n squares is,

`\sum_(i=1)^(n)n^2=(n(n+1)(2n+1))/(6) \\\\\implies\sum_(i=1)^(11)i^2=(11(11+1)(2* 11+1))/(6) =506`

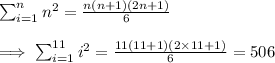
Step 3

In this step we use the result from step 1 to evaluate the sum.
`3\sum_(i=1)^(11)i^2-88=3(506)-88=1,430.`

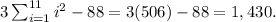
The correct answer is Option 4,which is 1,430.