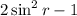Question

HELP! Convert this identity to one using sine terms only !

1-2 cos^2 r=
A. -1-sin^2r
B. 2sin^2r-1
C. 1-2sin^2t

Please explain!

Answer 1

option B is correct.

`2\sin^2r - 1`

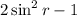
Explanation:

Given the expression:
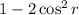`1-2\cos^2r` ......[1]

Using trigonometric identities:

`\sin^2r+ \cos^2r = 1`

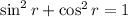
We can rearrange this as;

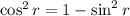`\cos^2r = 1-\sin^2r` ......[2]

Substitute equation [2] into [1] we get;

`1-2(1-\sin^2r)`

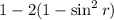
Using distributive property:
`a\cdot (b+c) = a \cdot b + a\cdot c`

`1- 2 +2sin^2r`

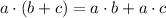
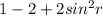
or

`-1+2\sin^2r`

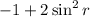
therefore, the given expression in terms of sine terms is;
`2\sin^2r-1`