Answer:
Option 2 - It is compressed horizontally by a factor of 2 and translated up 3.
Explanation:
Given : The graph
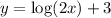 and
and
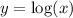
To find : How does the graph of
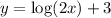 related to the graph of
related to the graph of
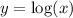
Solution :
The parent function be
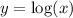
Horizontally Compressed:
If y =f(x) , then y =f(bx) gives a horizontal compression if b>1.
Multiplying the parent function by 2 means you are compressing it horizontally,
i,e
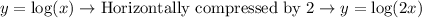
Translated up :
i.e, f(x)→f(x)+b
Adding 3 means you are moving it up by 3 units

Therefore, Option 2 is correct.
It is compressed horizontally by a factor of 2 and translated up 3.