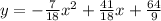Answer:
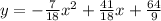
Explanation:
We need to write a quadratic equation so we can use standard quadratic equation:
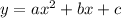
Plug the given points to get three equations.
for (7,4), we plug x=7 and y=4
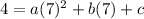
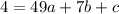 ...(i)
...(i)
similarly using other two points, we get:
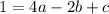 ...(ii)
...(ii)
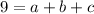 ...(iii)
...(iii)
Now we solve those three equations by any method like substitution, or matrices or by any method and get:
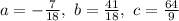
Now plug these values into
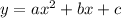 , we get final equation as:
, we get final equation as: