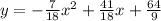Question

Write the quadratic equation in standard form for the following equations
(7,4);(-2,1);(1,9)

Answer 1

`y=-(7)/(18)x^2+(41)/(18)x+(64)/(9)`

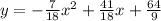
Explanation:

We need to write a quadratic equation so we can use standard quadratic equation:

`y=ax^2+bx+c`

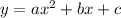
Plug the given points to get three equations.

for (7,4), we plug x=7 and y=4

`4=a(7)^2+b(7)+c`

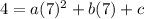
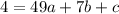`4=49a+7b+c` ...(i)

similarly using other two points, we get:

`1=4a-2b+c` ...(ii)

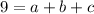`9=a+b+c` ...(iii)

Now we solve those three equations by any method like substitution, or matrices or by any method and get:

`a=-(7)/(18),\ b=(41)/(18),\ c=(64)/(9)`

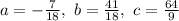
Now plug these values into
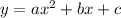`y=ax^2+bx+c`, we get final equation as:

`y=-(7)/(18)x^2+(41)/(18)x+(64)/(9)`