Question

Write the explicit formula for the geometric sequence.

64, 32, 16, 8, ...

A) an = 8 · 4n-1

B) an = 8 · 2n-1

C) an = 32 · 0.5n-1

D) an = 64 · 0.5n-1


Which answer?

Answer 1

Option D is correct.

Explicit formula for the geometric sequence is,
`a_n = 64 \cdot (0.5)^(n-1)`

Explanation:

Geometric sequence states that a sequence of numbers in which the ratio between consecutive terms is constant,

we can write a formula for the nth geometric sequence in the form of:

`a_n = a_1r^(n-1)` .....[1] where
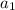`a_1` is the first term and r is the common ratio between successive term.

Given the sequence: 64, 32, 16 , 8......

Here, first term (
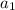`a_1`) = 64.

Common ratio(r) = 0.5

Since,

`(32)/(64) =0.5`

`(16)/(32) = 0.5` ,

`(8)/(16) = 0.5` ......

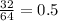
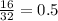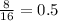Substitute the value of a and r in [1] we get;

`a_n = 64 \cdot (0.5)^(n-1)`

therefore, the explicit formula for the geometric sequence is,
`a_n = 64 \cdot (0.5)^(n-1)`