Answer:
1.
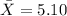
2.

3.
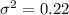
Explanation:
QUESTION 1
The given data set for the expenditure is
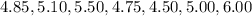
The formula for calculating the mean is given by,
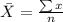
We need to add all the expenditure and divide by the total number of days.
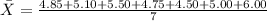
This gives us,
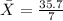
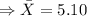 to the nearest hundredth.
to the nearest hundredth.
QUESTION 2
The standard deviation of the data set is given by the formula;
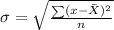
This implies that,
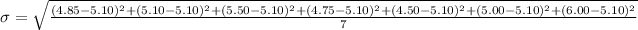
This will give us,
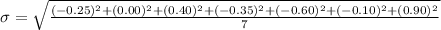
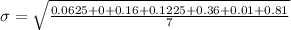
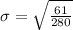
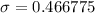
to the nearest hundredth,
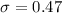 .
.
QUESTION 3
The variance is the square of the standard deviation.

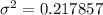
To the nearest hundred gives,
