Answer:
Wanda and Dave will catch each other in 54 seconds after Dave starts walking.
Explanation:
Let Wanda and Dave catch each other when x be the time after Dave starts walking and y be the distance covered by them
It is given that Wanda started walking along a path 27 seconds before Dave and the constant speed of Wanda is 3 feet per second.

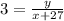

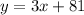 .... (1)
.... (1)
The constant speed of Dave is 4.5 feet per second.
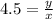
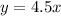 .... (2)
.... (2)
Equate equation (1) and (2).
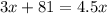
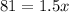
Divide both sides by 1.5.

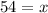
Therefore, Wanda and Dave will catch each other in 54 seconds after Dave starts walking.