Question

Divide (x^3-8x^2+17x-10)/(x-5)

Answer 1

`x^(2)-3x+2`

Explanation:

Use synthetic division.

• Reverse the sign of -5 and write the coefficients of the polynomial.
• Multiply the coefficient by the divisor, then add to the next coefficient.
• Continue through the last coefficient.

5 | 1 -8 17 -10

+ 5 -15 10

1 -3 2 0

The quotient is
`x^(2) -3x+2`.

Answer 2

(x - 2)*(x - 1) is the answer

Explanation:

We have to divide the polynomial f(x) = x^{3}-8x^{2}+17x-10 by (x-5).

Now, after dividing f(x) gets simplified into (x-5)*(x^{2}-3x+2).

So, we need to factorize the quadratic equation x^{2}-3x+2.

i.e. x^{2} - 3x + 2 = x^{2} - x - 2x + 2 = x(x-1) - 2(x-1) = (x - 2)*(x - 1)

Therefore, f(x) again gets simplified into (x-5)*(x - 2)*(x - 1)

Now eliminating the common factor (x-5).

We get,
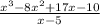`(x^(3)-8x^(2)+17x-10)/(x-5)` = (x - 2)*(x - 1)