Question

Solve each system by substitution. Tell whether the system has one solution, infinitely many solutions, or no solution.

3x+6y=18
3y=-3/2x+9

Answer 1

First, get one of the variables on its own. I'm going to do the first equation since it looks easier. :)


`3x + 6y = 18`
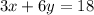
Subtract 6y from both sides.


`3x = 18 - 6y`
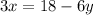
Divide both sides by 3 to get the variable alone.

`x = 6 - 2y`
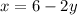
Plug this into the other equation for x.


`3y = - (3)/(2) (6 - 2y) + 9`
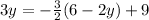
Distribute.


`3y = - 9 + 3y + 9`
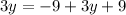
Add like terms.


`3y = 3y`
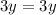
The system has infinitely many solutions because both sides equal each other.

Hope this helped!

:)