First, get one of the variables on its own. I'm going to do the first equation since it looks easier. :)
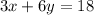
Subtract 6y from both sides.
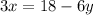
Divide both sides by 3 to get the variable alone.
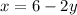
Plug this into the other equation for x.

Distribute.
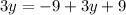
Add like terms.
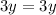
The system has infinitely many solutions because both sides equal each other.
Hope this helped!
:)