Answer:
The table which represents a linear function is:
Last table.
x y
1 -5
2 0
3 5
4 10
Explanation:
We know that a function is linear if the rate of change is constant.
i.e. the ratio of difference in y value to the corresponding difference in x value is constant.
i.e. for two values (x,y) and (x',y') the rate of change is given by:
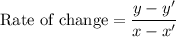
In each of the tables we observe that the difference in x-value is constant i.e. 1.
since, 2-1=1
3-2=1
and 4-3=1
Now, the function will be linear for which the difference in the y-value is constant.
a)
x y
1 5
2 9
3 5
4 9
The difference in the y-value is as follows:
9-5=4
5-9= -4
9-5= 4
Since, the difference is not constant.
Hence, the function is not linear.
b)
x y
1 -5
2 10
3 -15
4 20
The difference in the y-value is as follows:
10-(-5)=15
-15-10= -25
20-(-15)=35
Hence, the function is not linear ; since the difference in the y-value is not constant.
c)
x y
1 5
2 10
3 20
4 40
The difference in the y-value is as follows:
10-5=5
20-10=10
40-20=20
Since, the difference in the y-value is not constant.
Hence, the function is not linear.
d)
x y
1 -5
2 0
3 5
4 10
The difference in the y-value is as follows:
0-(-5)=5
5-0=5
10-5=5
Since, the difference in the y-value is constant.
Hence, the function is linear.