Question

Two sides of a triangle measure 9 cm and 23 cm. Which could be the measure of the third side of the triangle?

Answer 1

Hello,

Let's be x the length of the 3 side (9,x,23) ==>x>0

Using inequality triangular:

9<x+23==>x>9-23==>x>-14 (done)

x<9+23==>x<32

23<x+9==>x>14

SO 14<x<32

Answer 2

`14<x<32`

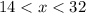
Explanation:

Let x be the third side of triangle.

We have been given that two sides of a triangle measure 9 cm and 23 cm. We are asked to find the measure of third side of triangle.

We will use triangle inequality theorem to solve our given problem.

Triangle inequality theorem states that sum of two sides of a triangle must be greater than third side of triangle.

Using triangle inequality theorem, we will get:

(1)
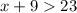
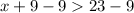
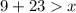
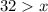
`x+9>23`

`x+9-9>23-9`

`x>14`

(2)
`9+23>x`

`32>x`

(3)
`x+23>9`

`x+23-23>9-23`

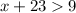
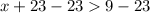
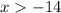`x>-14` (Not applicable as length cannot be negative).

Therefore, the measure of third side of triangle would be
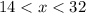`14<x<32`.