Answer:
The decibel level of this second sound is 48.021 decibels.
Explanation:
The acoustic intensity (
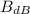 ), measured in decibels, is defined by the following formula:
), measured in decibels, is defined by the following formula:
 (1)
(1)
Where:
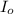 - Reference sound intensity, measured in watts per square meter.
- Reference sound intensity, measured in watts per square meter.
 - Real sound intensity, measured in watts per square meter.
- Real sound intensity, measured in watts per square meter.
If we know that
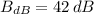 and
and
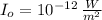 , then the real sound intensity of the first sound is:
, then the real sound intensity of the first sound is:
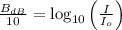
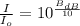
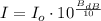
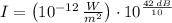

The real sound intensity of the second sound is four times greater, that is:
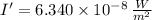
If we know that
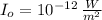 and
and
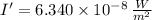 , then the acoustic intensity of the second sound is:
, then the acoustic intensity of the second sound is:
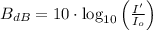
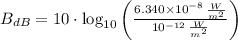
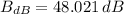
The decibel level of this second sound is 48.021 decibels.