Question

A sound measures 42 dB. The intensity of a second sound is four times as great. What is the decibel level of this

second sound?

Answer 1

The decibel level of this second sound is 48.021 decibels.

Explanation:

The acoustic intensity (
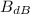`B_(dB)`), measured in decibels, is defined by the following formula:

`B_(dB) = 10\cdot \log_(10)\left((I)/(I_(o)) \right)` (1)

Where:

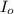`I_(o)` - Reference sound intensity, measured in watts per square meter.

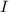`I` - Real sound intensity, measured in watts per square meter.

If we know that
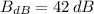`B_(dB) = 42\,dB` and
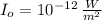`I_(o) = 10^(-12)\,(W)/(m^(2))`, then the real sound intensity of the first sound is:

`(B_(dB))/(10) = \log_(10)\left((I)/(I_(o)) \right)`

`(I)/(I_(o)) = 10^{(B_(dB))/(10) }`

`I = I_(o)\cdot 10^{(B_(dB))/(10) }`

`I = \left(10^(-12)\,(W)/(m^(2)) \right)\cdot 10^{(42\,dB)/(10) }`

`I = 1.585* 10^(-8)\,(W)/(m^(2))`

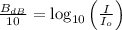
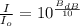
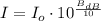
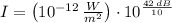
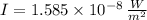
The real sound intensity of the second sound is four times greater, that is:

`I' = 6.340* 10^(-8)\,(W)/(m^(2))`

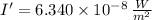
If we know that
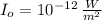`I_(o) = 10^(-12)\,(W)/(m^(2))` and
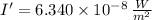`I' = 6.340* 10^(-8)\,(W)/(m^(2))`, then the acoustic intensity of the second sound is:

`B_(dB) = 10\cdot \log_(10)\left((I')/(I_(o)) \right)`

`B_(dB) = 10\cdot \log_(10)\left((6.340* 10^(-8)\,(W)/(m^(2)) )/(10^(-12)\,(W)/(m^(2)) ) \right)`

`B_(dB) = 48.021\,dB`

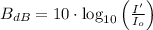
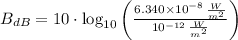
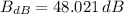
The decibel level of this second sound is 48.021 decibels.