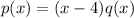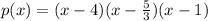Question

The polynomial p(x)=3x^3-20x^2+37x-20 has a known factor of (x-4). Rewrite p(x) as a product of linear factors. p(x) =

Answer 1

Answer: (x-4)(3x-5)(x-1)

Explanation:

Answer 2

`p(x) = (x-4)(x - (5)/(3))(x - 1)`

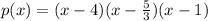
Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

This polynomial has roots
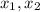`x_(1), x_(2)` such that
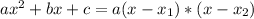`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

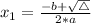
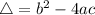
In this question:

We have the polynomial
`p(x) = 3x^3-20x^2+37x-20`

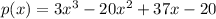
It has a known factor
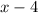`x - 4`. This means that the polynomial can be written as:

`p(x) = (x-4)q(x)`

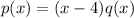
In which q(x) is a second order polynomial, because p is of the third degree and q is of the first degree(3 - 1 = 2). So

`q(x) = ax^2 + bx + c`

We have to find a, b and c. Then

`3x^3-20x^2+37x-20 = (x-4)(ax^2 + bx + c)`

`3x^3-20x^2+37x-20 = = ax^3 + (-4a + b)x^2 + (c - 4b)x - 4c`

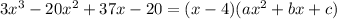
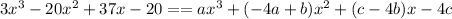
Comparing both sides, we have that

`a = 3`

`-4c = -20 \rightarrow c = 5`

`c - 4b = 37`

`-4b = 32 \rightarrow b = -8`

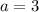
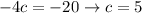
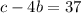
Now we find the roots of this polynomial.

`\bigtriangleup = b^(2) - 4ac = (-8)^2 - 4(3)(5) = 64 - 60 = 4`

`x_(1) = (-(-8) + √(4))/(2*3) = (5)/(3)`

`x_(2) = (-(-8) - √(4))/(2*3) = 1`

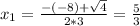
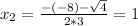
So, as a product of it's factors, we have that q is:

`q(x) = (x - (5)/(3))(x - 1)`

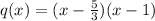
And p(x)

`p(x) = (x-4)q(x)`

`p(x) = (x-4)(x - (5)/(3))(x - 1)`