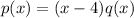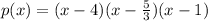Answer:
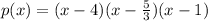
Explanation:
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
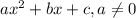 .
.
This polynomial has roots
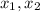 such that
such that
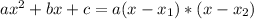 , given by the following formulas:
, given by the following formulas:
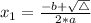
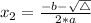
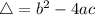
In this question:
We have the polynomial
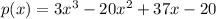
It has a known factor
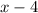 . This means that the polynomial can be written as:
. This means that the polynomial can be written as:
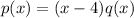
In which q(x) is a second order polynomial, because p is of the third degree and q is of the first degree(3 - 1 = 2). So
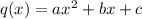
We have to find a, b and c. Then
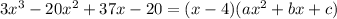
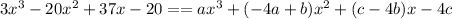
Comparing both sides, we have that
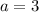
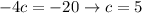
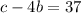
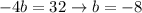
Now we find the roots of this polynomial.

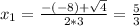
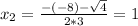
So, as a product of it's factors, we have that q is:
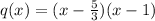
And p(x)