Question

Find the median, range, and interquartile range of both sets: Set 1: 65, 66, 77, 79, 81, 93, 104, 105 Set 2: 56, 1, 29, 72, 67, 59, 74, 60 Which is true about the two sets?

A.Set 1 has a range of 40 and a median of 85.
B.Set 2 has a range of 74 and a median of 62
C.Both sets have an interquartile range of 27
D.Set 2 has data that is closer to its median than Set 1.

Answer 1

c

Explanation:

Answer 2

Option c. Both sets have an interquartile range of 27.

Explanation:

To find median first we write both the sets in ascending order.

Set 1: 65, 66, 77, 79, 81, 93, 104, 105

Median is the middle number of the set or mean of two middle numbers. Median =
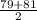`(79+81)/(2)` = 80

Range = highest - lowest

Range = 105 - 65 = 40

IQR = Median of upper quartile - Median of lower quarlile

QR = Q3 - Q1

IQR = 98.5 - 71.5 = 27

Set 1 : Median = 80, Range = 40, IQR = 27

Set 2: 1, 29, 56, 59, 60, 67, 72, 74

Median =
`(59+60)/(2)` = 59.5

Range = 74 - 1 = 73

IQR = 69.5 - 42.5 = 27

Set 2 : Median = 59.5, Range = 73, IQR = 27

Option c. is correct Both sets have an interquartile range of 27.