Question

The angle of elevation from a soccer ball on the ground to the top of the goal is 34. If the goal is 8 feet tall, What is the distance from he ball to the goal?

Answer 1

The distance from he ball to the goal is 11.85 feet (Approx) .

Explanation:

As given

The angle of elevation from a soccer ball on the ground to the top of the goal is 34° .

If the goal is 8 feet tall.

Now by using the trigonometric identity .

`tan \theta = (Perpendicular)/(Base)`

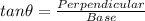
As shown in the diagram given below

`\theta = 34^(\circ)`

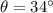
Perpendicular = AB = 8 feet

Base = BC

Put all the values in the identity .

`tan\ 34^(\circ) = (AB)/(BC)`

`tan\ 34^(\circ) = (8)/(BC)`

`tan\ 34^(\circ) = 0.675\ (Approx)`

`BC = (8)/(0.675)`

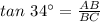
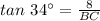
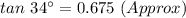
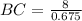
BC = 11.85 feet (Approx)

Therefore the distance from he ball to the goal is 11.85 feet (Approx) .