What is the slope of a line perpendicular to the line whose equation is x - 3y = -18. Fully reduce your answer.

Question

asked Jan 20, 2022 170k views

1 Answer

Jins Thomas Shaji · Answer 1 · 2022-01-26T13:33:01+0000

Given:

Equation of a line is

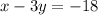
x-3y=-18

To find:

The slope of the line perpendicular to the given line.

Solution:

The slope of the equation
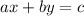ax+by=c is

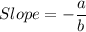
Slope=-(a)/(b)

We have,

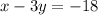
x-3y=-18

Here, a=1, b=-3. So, slope of this line is

m_1=-(1)/(-3)

m_1=(1)/(3)

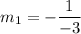
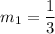
Product of slopes of two perpendicular lines is -1.

Let slope of perpendicular line is
m_2 .

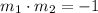
$m_1\cdot m_2=-1$

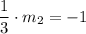
$(1)/(3)\cdot m_2=-1$

m_2=-3

Therefore, the slope of the perpendicular line is -3.