Question

A kite is 37 feet in the air and string forms an angle of 62 degrees with the ground how long is the string

Answer 1

The length of the string is 32.56 feet (Approx) .

Explanation:

As given

A kite is 37 feet in the air and string forms an angle of 62 degrees .

Now by using the trignometric identity.

`sin\theta = (Perpendicular)/(Hypotenuse)`

As shown in the figure given below.

`\theta = 62^(\circ)`

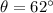
Perpendicular = AB

Hypotenuse = AC = 37 feet

Put in the identity .

`sin\ 62^(\circ) = (AB)/(AC)`

`sin\ 62^(\circ) = (AB)/(37)`

`sin\ 62^(\circ) = 0.88\ (Approx)`

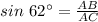
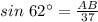
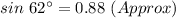
Put in the identity

`0.88 = (AB)/(37)`

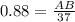
AB = 0.88 × 37

AB = 32.56 feet (Approx)

Therefore the length of the string is 32.56 feet (Approx) .