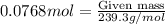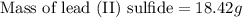Question

How many grams of lead ii sulfide is produced when 25.0 g lead ii acetate reacts with excess hydrogen sulfide

Answer 1

Answer: 18.42 grams of lead (II) sulfide will be produced in the given reaction:

Explanation: The reaction of lead (II) acetate and hydrogen sulfide follows:

`(CH_3COO)_2Pb+H_2S\rightarrow PbS+2CH_3COOH`

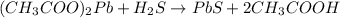
To calculate the moles, we use the formula:

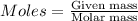`Moles=\frac{\text{Given mass}}{\text{Molar mass}}` ....(1)

Molar mass of lead (II) acetate = 325.29 g/mol

Given mass of lead (II) acetate = 25 g

Putting values in above equation, we get:

`Moles=(25g)/(325.29g/mol)=0.0768moles`

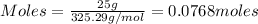
We are given that hydrogen sulfide is present in excess, so limiting reagent is lead (II) acetate because it limits the formation of product.

By stoichiometry of the reaction,

1 moles of lead (II) acetate produces 1 mole of lead (II) sulfide

So, 0.0768 moles of lead (II) acetate will produce =
`(1)/(1)* 0.0768` = 0.0768 moles of lead (II) sulfide.

Now, to calculate the mass of lead (II) sulfide, we use equation 1, we get:

Molar mass of lead (II) sulfide = 239.3 g/mol

`0.0768mol=\frac{\text{Given mass}}{239.3g/mol}`

`\text{Mass of lead (II) sulfide}=18.42g`