Answer:
ω = 7 x 10¹⁵ rev/s
Step-by-step explanation:
The linear and angular velocities are related through the following formula:
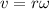
where,
v = linear speed of electron = 2200000 m/s
r = radius of orbit =
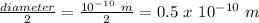
therefore, substituting these values in the formula, we get:
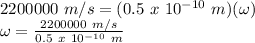
ω = 4.4 x 10¹⁶ rad/s
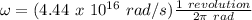
ω = 7 x 10¹⁵ rev/s