Question

ΔABC is similar to ΔDEF. The ratio of the perimeter of ΔABC to the perimeter of ΔDEF is 2 : 11. If the longest side of ΔABC measures 15 units, what is the length of the longest side of ΔDEF?

Answer 1

82.5 cm

Explanation:

For similar triangles, ratio of perimeter will equal to ratio of sides.

Here we are given that triangles ABC and DEF are similar.

This implies the corresponding sides are proportional.

By corresponding we mean that the longest sides of ABC with the longest side of DEF.

Hence Longest side of ABC/Longest side of DEF = Ratio of sides

= Ratio of perimeter.

Let the longest side of DEF be x.

i.e. 15/x = 2/11

Cross multiply to get

2x = 165

Divide by 2

x = 82.5 cm.

Hence the longest side of Triangle DEF = 82.5 cm.

Verify: Check proportions of longest sides

=
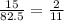`(15)/(82.5) =(2)/(11)` which equals ratio of perimeters.

Thus verified.