Answer:
Option A. (150√3- 75π) ft².
Explanation:
In the given picture a circle is inscribed in a regular hexagon with a side length = 10 feet.
Formula of the area of a regular hexagon
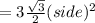
=
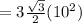
= 3√3×50 = 150×√3 feet²
Now we will calculate the area of circle inscribed.
Already given in the question that In a 30-60-90 triangle
Longer leg of triangle r = x√3 =
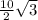 = 5√3 feet
= 5√3 feet
Now area of circle = π r² = π(5√3)² = 75π feet²
Area of shaded part = Area of Hexagon-Area of circle inscribed.
= (150√3 - 75π) ft²