Answer:
The coordinates of orthocenter of the triangle are (1,5).
Explanation:
The given vertices are A(0,6), B(4,6) and C(1,3).
Orthocenter of a triangle is the intersection point of all altitudes.
The product of slopes of two perpendicular lines is -1.
The slope of AB is
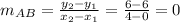
The slope of AB is 0, therefore slope of line which is perpendicular to AB is
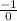 .
.
Point slope form of a line is
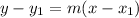
Where, m is the slope.
The equation of altitude on AB form C is
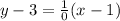
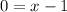
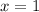 ..... (1)
..... (1)
Slope of BC is
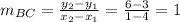
The slope of BC is 1 therefore the slope of altitude on BC from A is -1.
The equation of altitude on BC from A is
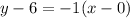
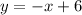 ..... (2)
..... (2)
Using (1) and (2) we get
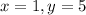
The intersection point of two altitudes is (1,5). Therefore coordinates of orthocenter of the triangle are (1,5).